RSA Algorithm
The pioneering paper by Diffie and Hellman introduced a new approach to cryptography and, in effect, challenged cryptologists to come up with a cryptographic algorithm that met the requirements for public-key systems. A number of algorithms have been proposed for public-key cryptography. Some of these, though initially promising, turned out to be breakable.
One of the first successful responses to the challenge was developed in 1977 by Ron Rivest, Adi Shamir, and Len Adleman at MIT and first published in 1978.The Rivest-Shamir-Adleman (RSA) scheme has since that time reigned supreme as the most widely accepted and implemented general-purpose approach to public-key encryption.
The RSA scheme is a block cipher in which the plaintext and ciphertext are integers between 0 and $n - 1$ for some $n$.A typical size for $n$ is 1024 bits, or 309 decimal digits. That is, $n$ is less than $2^{1024}$.
Description of the Algorithm
RSA makes use of an expression with exponentials. Plaintext is encrypted in blocks, with each block having a binary value less than some number $n$.That is, the block size must be less than or equal to $log_2(n) + 1$; in practice, the block size is $i$ bits, where $2^i < n ≤ 2^{i+1}$. Encryption and decryption are of the following form, for some plaintext block $M$ and ciphertext block $C$.
$$C = M^e \pmod{n}$$
$$M = C^d \pmod{n} = (M^e)^d \pmod{n} = M^{ed} \pmod{n}$$
Both sender and receiver must know the value of $n$. The sender knows the value of $e$, and only the receiver knows the value of $d$. Thus, this is a public-key encryption algorithm with a public key of $PU = \{e, n\}$ and a private key of $PR = \{d, n\}$.For this algorithm to be satisfactory for public-key encryption, the following requirements must be met.
1. It is possible to find values of $e, d, n$ such that $M^{ed} \pmod{n} = M$ for all $M < n$.
2. It is relatively easy to calculate $M^e \pmod{n}$ and $C^d \pmod{n}$ for all values of $M < n$.
3. It is infeasible to determine $d$ given $e$ and $n$.
For now, we focus on the first requirement and consider the other questions later.We need to find a relationship of the form
$$M^{ed} \pmod{n} = M$$
The preceding relationship holds if $e$ and $d$ are multiplicative inverses modulo $\phi(n)$, where $\phi(n)$ is the Euler totient function. It is known that for $p,q$ prime, $\phi(pq) = (p - 1)(q - 1)$. The relationship between $e$ and $d$ can be expressed as
$$ed \equiv 1\pmod{\phi(n)}$$
$$d \equiv e^{-1} \pmod{\phi(n)}$$
That is, $e$ and $d$ are multiplicative inverses $\pmod {\phi(n)}$. Note that, according to the rules of modular arithmetic, this is true only if $d$ (and therefore $e$) is relatively prime to $\phi(n)$. Equivalently, $gcd(\phi(n), d) = 1$.
We are now ready to state the RSA scheme.The ingredients are the following:
$p, q$, two prime numbers (private, chosen)
$n = pq$ (public, calculated)
$e$, with $gcd(\phi(n), e) = 1; 1 < e < \phi(n)$ (public, chosen)
$d \equiv e^{-1} \pmod {\phi(n)}$ (private, calculated)
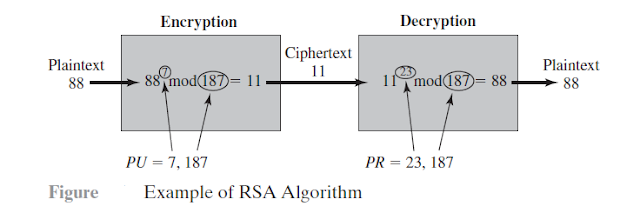
The private key consists of $\{d, n\}$ and the public key consists of $\{e, n\}$. Suppose that user $A$ has published its public key and that user $B$ wishes to send the message $M$ to $A$.Then $B$ calculates $C = M^e \pmod{n}$ and transmits $C$. On receipt of this ciphertext, user $A$ decrypts by calculating $M = C^d \pmod{n}$. Figure below summarizes the RSA algorithm.Alice generates a public/private key pair; Bob encrypts using Alice’s public key; and Alice decrypts using her private key.
Example
1. Select two prime numbers, $p = 17$ and $q = 11$.
2. Calculate $n = pq = 17 × 11 = 187$.
3. Calculate $\phi(n) = (p - 1)(q - 1) = 16 × 10 = 160$.
4. Select $e$ such that $e$ is relatively prime to $\phi(n) = 160$ and less than $\phi(n)$; we
choose $e = 7$.
5. Determine $d$ such that $d \times e \equiv 1 \pmod {160}$ and $d < 160$.The correct value is $d = 23$,because $23 × 7 = 161 = (1 × 160) + 1$; $d$ can be calculated using the extended Euclid’s algorithm.
The resulting keys are public key $PU = \{7, 187\}$ and private key $PR = \{23, 187\}$.
Consider a plaintext input of $M= 88$. For encryption, we need to calculate
$C = 88^7 \pmod {187}=11$
For decryption, we calculate $M = 11^{23} \pmod{187}=88$
from sympy import mod_inverse
# Function to generate public and private keys
def generate_keys():
# Choose two distinct prime numbers (small values for demonstration)
p=17
q=11
# Compute n = p * q
n = p * q
# Compute Euler's totient function, phi(n) = (p-1) * (q-1)
phi = (p - 1) * (q - 1)
# Choose an integer e such that 1 < e < phi(n) and gcd(e, phi(n)) = 1
e = 7
# Common choice for e is 65537, but we use a smaller number for simplicity
# Compute the modular inverse of e, d = e^(-1) mod phi(n)
d = mod_inverse(e, phi)
print("p=",p,"q=",q,"n=",n)
print(f"Public Key(e={e},n={n})")
print(f"Private Key(d={d},n={n})")
# Public key (e, n) and private key (d, n)
return (e, n), (d, n)
# Function to encrypt a message using the public key
def encrypt(M, public_key):
e, n = public_key
C = pow(M, e, n)
return C
# Function to decrypt a message using the private key
def decrypt(C, private_key):
d, n = private_key
decrypted_message = pow(C, d, n)
return decrypted_message
# Example usage
public_key, private_key = generate_keys()
M = 88
print(f"Original message: {M}")
# Encrypt the message
C = encrypt(M, public_key)
print(f"Encrypted message: {C}")
# Decrypt the message
decrypted_message = decrypt(C, private_key)
print(f"Decrypted message: {decrypted_message}")
Output
p= 17 q= 11 n= 187 Public Key(e=7,n=187)
Private Key(d=23,n=187)
Original message: 88
Encrypted message: 11
Decrypted message: 88
We now look at an example , which shows the use of RSA to process multiple blocks of data. In this simple example, the plaintext is an alphanumeric string. Each plaintext symbol is assigned a unique code of two decimal digits (e.g., a = 00, A = 26).A plaintext block consists of four decimal digits, or two alphanumeric characters. Figure-a illustrates the sequence of events for the encryption of multiple blocks, and Figure-b gives a specific example. The circled numbers indicate the order in which operations are performed.
Python Code RSA
from sympy import mod_inverse
from sympy import randprime
# Function to generate public and private keys
def generate_keys():
# Choose two distinct prime numbers (small values for demonstration)
p=randprime(11,100)
q=randprime(p,200)
# Compute n = p * q
n = p * q
# Compute Euler's totient function, phi(n) = (p-1) * (q-1)
phi = (p - 1) * (q - 1)
# Choose an integer e such that 1 < e < phi(n) and gcd(e, phi(n)) = 1
e = 17
# Common choice for e is 65537, but we use a smaller number for simplicity
# Compute the modular inverse of e, d = e^(-1) mod phi(n)
d = mod_inverse(e, phi)
print("p=",p,"q=",q,"n=",n)
print(f"Public Key(e={e},n={n})")
print(f"Private Key(d={d},n={n})")
# Public key (e, n) and private key (d, n)
return (e, n), (d, n)
# Function to encrypt a message using the public key
def encrypt(message, public_key):
e, n = public_key
encrypted_message = [pow(ord(char), e, n) for char in message]
return encrypted_message
# Function to decrypt a message using the private key
def decrypt(encrypted_message, private_key):
d, n = private_key
decrypted_message = ''.join(chr(pow(char, d, n)) for char in encrypted_message)
return decrypted_message
# Example usage
public_key, private_key = generate_keys()
message = "HELLO"
print(f"Original message: {message}")
# Encrypt the message
encrypted_message = encrypt(message, public_key)
print(f"Encrypted message: {encrypted_message}")
# Decrypt the message
decrypted_message = decrypt(encrypted_message, private_key)
print(f"Decrypted message: {decrypted_message}")
Output:
p= 83 q= 163 n= 13529
Public Key(e=17,n=13529)
Private Key(d=9377,n=13529)
Original message: HELLO
Encrypted message: [9939, 4273, 13255, 13255, 107]
Decrypted message: HELLO
Output:
p= 83 q= 163 n= 13529
Public Key(e=17,n=13529)
Private Key(d=9377,n=13529)
Original message: HELLO
Encrypted message: [9939, 4273, 13255, 13255, 107]
Decrypted message: HELLO
The Mathematics Behind Why It Works
The critical mathematical property that makes RSA work is based on modular arithmetic and the properties of prime numbers.
Why does decryption recover the original message?
The decryption step works because of the following relationship:
This can be rewritten as:
Since , there exists an integer such that:
Thus:
By Euler's theorem, for any integer that is relatively prime to :
So:
$$M^{k\phi(n)} \equiv 1 \, (\text{mod} \, n)$$Thus:
$$M^{ed} \equiv M \times 1 \equiv M \, (\text{mod} \, n)$$This shows that after applying the decryption process, we recover the original message .
Example ( University Question)
Explain in detail about RSA algorithm.Given p=7,q=11,e=17, M=8 encrypt using RSA
p= 7 q= 11 n= 77$\phi(n)=6 \times 10 = 60$
$d \times e \equiv 1 \pmod {60}$
$d \times 17 \equiv 1 \pmod {60}$
$d=53$
Public Key(e=17,n=77)
Private Key(d=53,n=77)
Ecryption=$M^e \pmod{n}=8^{17} \pmod{60}=57$



Comments
Post a Comment